Second Order System Response

System Transfer Function

The transfer function \(H(s)\) for a second-order system is:

\[H(s) = \frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}\]

where:

• \(\zeta\) is the damping ratio
• \(\omega_n\) is the natural frequency

Response Types

The system exhibits three characteristic behaviors:

1. Underdamped (\(\zeta < 1\))
   • System oscillates with decreasing amplitude
   • Common in systems with insufficient damping
2. Critically Damped (\(\zeta = 1\))
   • Fastest return to steady state without oscillation
   • Optimal for many control applications
3. Overdamped (\(\zeta > 1\))
   • Returns to steady state without oscillation
   • Slower response than critically damped

Interactive Plot

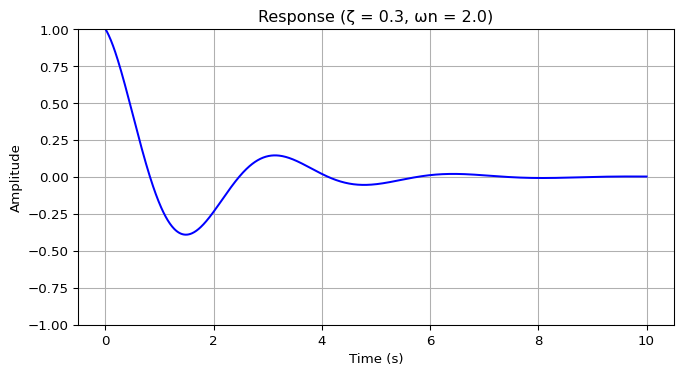
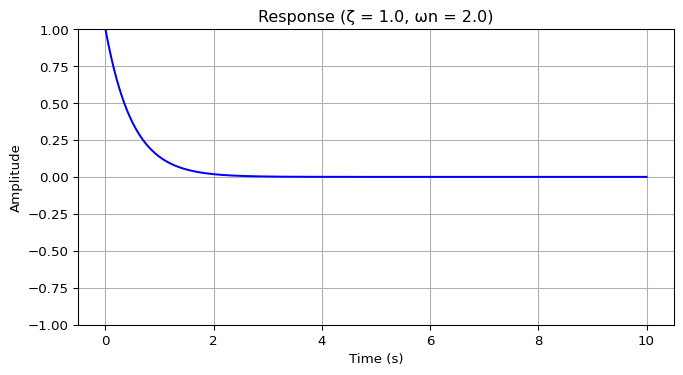
viewof dampingRatio = Inputs.range([0, 2], {
  value: 1.2,
  step: 0.1,
  label: "Damping ratio (ζ)"
})

viewof naturalFreq = Inputs.range([0.1, 5], {
  value: 3.4,
  step: 0.1,
  label: "Natural frequency (ωn)"
})

data = {
  const t = Array.from({length: 1000}, (_, i) => i * 0.01);
  return t.map(t => ({
    t,
    y: Math.exp(-dampingRatio * naturalFreq * t) * 
       Math.cos(naturalFreq * Math.sqrt(Math.max(0, 1 - dampingRatio**2)) * t)
  }));
}

Plot.plot({
  width: 800,
  height: 500,
  grid: true,
  x: {
    label: "Time (s)",
    domain: [0, 10]
  },
  y: {
    label: "Amplitude",
    domain: [-1, 1]
  },
  marks: [
    Plot.line(data, {
      x: "t",
      y: "y",
      stroke: "blue"
    })
  ]
})

Second Order Systems

• Model many physical and control systems
• Characterized by two parameters:
  • Damping ratio (ζ)
  • Natural frequency (ωn)

Transfer Function

The system is described by:

\[H(s) = \frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}\]

Key parameters:

• \(\zeta\) controls oscillation behavior
• \(\omega_n\) determines response speed
• Together they shape system dynamics

Response Types

Three characteristic behaviors based on damping ratio:

1. Underdamped (\(\zeta < 1\))
   • Oscillates with decreasing amplitude

2. Critically Damped (\(\zeta = 1\))
   • Fastest non-oscillatory response

3. Overdamped (\(\zeta > 1\))
   • Slow return to steady state

Underdamped Response

Characteristics:

• \(\zeta < 1\)
• Oscillatory behavior
• Common in practice

Critically Damped Response

Characteristics:

• \(\zeta = 1\)
• No oscillation
• Fastest settling

Overdamped Response

Characteristics:

• \(\zeta > 1\)
• No oscillation
• Slower response

Applications

• Mechanical Systems
  • Suspension systems
  • Vibration dampers
• Control Systems
  • Motor position control
  • Temperature regulation
• Electronic Systems
  • RLC circuits
  • Filters

Summary

Key takeaways:

• Second order systems are fundamental
• Damping ratio determines response type
• Natural frequency affects response speed
• Design involves balancing speed vs. stability